Moment of Inertia, Section Modulus, and Structural Design
- Share
- publisher
- Tianjin Yuantai Derun steel pipe manufacturing group Ltd.
- Issue Time
- Sep 18,2023
Summary
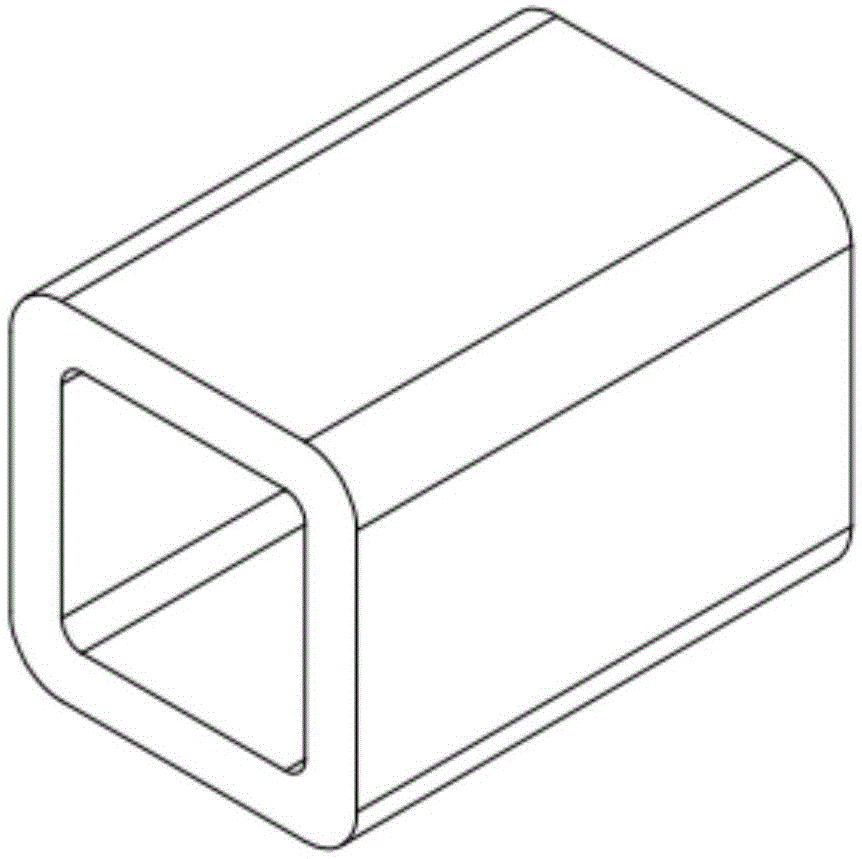
Moment of Inertia and Section Modulus of Square and Rectangular Tubes
Introduction
In engineering and structural design, understanding the properties of different shapes is crucial. Two important parameters used to evaluate the strength and rigidity of square and rectangular tubes are the moment of inertia and section modulus. These measures provide insights into how these tubes perform under different types of loads and help engineers make informed design decisions.
Understanding Moment of Inertia and Section Modulus
Before diving into the specifics of square and rectangular tubes, let's understand what moment of inertia and section modulus mean.
**Moment of Inertia** is a measure of an object's resistance to changes in its rotational motion around a particular axis. It quantifies how mass is distributed around that axis. In simpler terms, it tells us how difficult it is to rotate an object about a given axis.
**Section Modulus**, on the other hand, measures a beam's ability to resist bending. It indicates the strength of a structural member in resisting deformation due to applied loads.
Moment of Inertia for Square Tubes
To calculate the moment of inertia for a square tube, we need to consider its dimensions and the distribution of mass within it. The formula for the moment of inertia of a solid square tube is given by:
$I_{xx} = (a^4 - b^4)/12
Where:
- $I_{xx}$ is the moment of inertia about the x-axis
- $a$ is the length of one side of the square tubes
- $b$ is the length of one side of the inner hollow square (if present)
Section Modulus for Square Tubes
The section modulus of a square tube determines its ability to resist bending stresses. It is calculated using the following formula:
S_(xx)=(a^4-b^4)/6a
Where:
- $S_{xx}$ is the section modulus about the x-axis
- $a$ is the length of one side of the square
- $b$ is the length of one side of the inner hollow square (if present)
Moment of Inertia and Section Modulus for Rectangular Tubes
Similar to square tubes, the moment of inertia and section modulus can also be determined for rectangular tubes. The formulas are slightly different due to the varying dimensions. For a solid rectangular tube, the formulas are as follows:
$S_{xx} = (bh^3)/12
Where:
- $I_{xx}$ is the moment of inertia about the x-axis
- $S_{xx}$ is the section modulus about the x-axis
- $a$ is the length of one side of the rectangle
- $b$ is the length of the other side of the rectangle
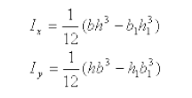
Moment of Inertia and Section Modulus for Hollow Rectangular Tubes
When dealing with hollow rectangular tubes, the formulas for moment of inertia and section modulus are modified to account for the presence of an inner hollow region. The formulas are as follows:
$I_{xx} = \frac{(a^4 - b^4) - (c^4 - d^4)}{12}$
$S_{xx} = \frac{(a^3 - b^3) - (c^3 - d^3)}{6}$
Where:
- $I_{xx}$ is the moment of inertia about the x-axis
- $S_{xx}$ is the section modulus about the x-axis
- $a$ is the length of the outer side of the rectangle
- $b$ is the length of the inner side of the outer rectangle
- $c$ is the length of the outer side of the inner rectangle
- $d$ is the length of the inner side of the inner rectangle
Moment of Inertia and Section Modulus for Hollow Square Tubes
For hollow square tubes, the formulas for moment of inertia and section modulus are similar to those of hollow rectangular tubes. The only difference lies in the fact that the sides of the square are equal. The formulas are as follows:
$I_{xx} = \frac{(a^4 - b^4)}{12}$
$S_{xx} = \frac{(a^3 - b^3)}{6}$
Where:
- $I_{xx}$ is the moment of inertia about the x-axis
- $S_{xx}$ is the section modulus about the x-axis
- $a$ is the length of the outer side of the square
- $b$ is the length of the inner side of the square
Conclusion
Moment of inertia and section modulus are vital parameters when it comes to evaluating the strength and rigidity of square and rectangular tubes. By understanding these concepts and utilizing the appropriate formulas, engineers can make informed design decisions that ensure the structural integrity and performance of their projects.
FAQs
What is the moment of inertia?
Moment of inertia quantifies an object's resistance to rotational motion around a particular axis.
What is section modulus?
Section modulus measures a beam's ability to resist bending.
Are the moment of inertia and section modulus the same for all shapes?
No, the formulas vary depending on the shape and dimensions of the object.
How are the moment of inertia and section modulus calculated for hollow tubes?
The formulas take into account the dimensions of the outer and inner sections of the tube.
Why are moment of inertia and section modulus important in engineering?
- These parameters help engineers evaluate the strength and rigidity of structural members and make informed design decisions.